https://magazine.sebastianraschka.com/p/understanding-and-coding-self-attention 글 번역했습니다.
이 게시글에서는 트랜스포머 아키텍처와 GPT-4, Llama와 같은 대규모 언어 모델(LLM)에서 사용되는 자기 주의 메커니즘에 대해 설명합니다. 자기 주의와 관련된 메커니즘은 LLM의 핵심 구성 요소로, 이러한 모델을 다루는 데 있어 이해하는 것이 유용한 주제입니다.
그러나 단순히 자기 주의 메커니즘을 논의하는 대신, Python과 PyTorch를 사용하여 기본부터 코딩해 보겠습니다. 제 생각에 알고리즘, 모델, 기술을 기본부터 코딩하는 것은 학습에 매우 효과적인 방법입니다!
참고로, 이 글은 옛 블로그에 게시한 "Understanding and Coding the Self-Attention Mechanism of Large Language Models From Scratch"의 현대화 및 확장판입니다. 저는 'from scratch' 방식으로 글을 쓰는 것(그리고 읽는 것)을 정말 좋아하기 때문에, 이 글을 Ahead of AI를 위해 현대화하기로 결정했습니다.
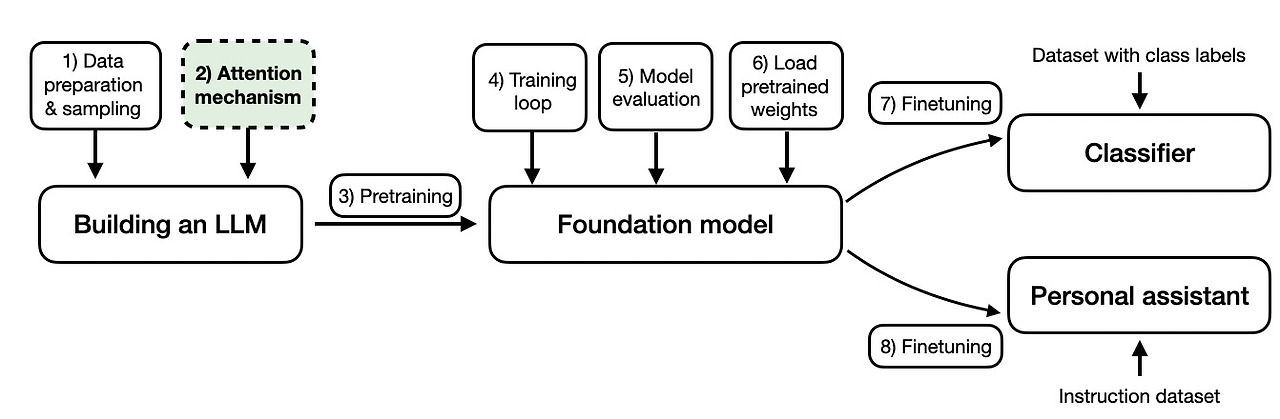
Introducing Self-Attention
원본 트랜스포머 논문(Attention Is All You Need)을 통해 소개된 이후로, Self-Attention은 특히 자연어 처리(NLP) 분야에서 많은 최첨단 딥러닝 모델의 핵심 요소로 자리 잡았습니다. 이제 자기 주의가 널리 사용되고 있기 때문에, 그 작동 원리를 이해하는 것이 중요합니다.

딥 러닝에서의 "attention" 개념은 재귀 신경망(RNN)을 더 긴 시퀀스나 문장을 처리하기 위해 개선하려는 노력에서 비롯되었습니다. 예를 들어, 한 언어에서 다른 언어로 문장을 번역하는 경우를 생각해 보세요. 문장을 단어별로 번역하는 것은 일반적으로 적합하지 않습니다. 왜냐하면 이는 각 언어에 고유한 복잡한 문법 구조와 관용구를 무시하기 때문에 부정확하거나 의미 없는 번역을 초래하기 때문입니다.

이 문제를 해결하기 위해 각 시간 단계에서 모든 시퀀스 요소에 접근할 수 있도록 주의 메커니즘이 도입되었습니다. 핵심은 특정 맥락에서 가장 중요한 단어를 선택적으로 결정하는 것입니다. 2017년 트랜스포머 아키텍처는 RNN을 완전히 제거하기 위해 독립적인 자기 주의 메커니즘을 도입했습니다.
(간결성을 위해, 그리고 이 기사가 기술적인 자기 주의 메커니즘 세부 사항에 집중할 수 있도록, 이 배경 동기부여 섹션을 간결하게 유지하겠습니다. 이를 통해 코드 구현에 집중할 수 있습니다.)

Self-Attention은 입력 임베딩의 정보량을 입력의 맥락에 대한 정보를 포함함으로써 향상시키는 메커니즘으로 볼 수 있습니다. 즉, 자기 주의 메커니즘은 모델이 입력 시퀀스 내의 다양한 요소들의 중요도를 평가하고 출력에 미치는 영향을 동적으로 조정할 수 있도록 합니다. 이는 단어의 의미가 문장이나 문서 내의 맥락에 따라 변할 수 있는 언어 처리 작업에서 특히 중요합니다.
자기 주의에는 많은 변형이 존재합니다. 특히 자기 주의를 더 효율적으로 만드는 데 많은 연구가 진행되었습니다. 그러나 대부분의 논문은 여전히 Attention Is All You Need 논문에서 소개된 원본 스케일드 닷 프로덕트 주의 메커니즘을 구현합니다. 이는 대부분의 기업이 대규모 트랜스포머를 훈련할 때 자기 주의가 계산적 병목 현상이 되기 어렵기 때문입니다.
따라서 이 기사에서는 실용적으로 가장 인기 있고 널리 사용되는 주의 메커니즘인 원본 스케일드 닷 프로덕트 주의 메커니즘(자기 주의라고도 함)에 초점을 맞춥니다. 그러나 다른 유형의 주의 메커니즘에 관심이 있다면 2020년 'Efficient Transformers: A Survey', 2023년 'A Survey on Efficient Training of Transformers' 리뷰, 그리고 최근의 FlashAttention과 FlashAttention-v2 논문을 참고하시기 바랍니다.
Embedding an Input Sentence
시작하기 전에, Self-Attention 메커니즘을 적용하려는 입력 문장 "Life is short, eat dessert first"를 고려해 보겠습니다. 텍스트 처리용 다른 모델링 접근 방식(예: 재귀 신경망이나 컨볼루션 신경망 사용)과 마찬가지로, 먼저 문장 임베딩을 생성합니다.
간단함을 위해 여기서는 사전 dc를 입력 문장에 등장하는 단어들로 제한합니다. 실제 응용 사례에서는 훈련 데이터셋에 포함된 모든 단어를 고려해야 하며(일반적인 어휘 크기는 30,000~50,000개 정도입니다).
In:
sentence = 'Life is short, eat dessert first'
dc = {s:i for i,s
in enumerate(sorted(sentence.replace(',', '').split()))}
print(dc)Out:
{'Life': 0, 'dessert': 1, 'eat': 2, 'first': 3, 'is': 4, 'short': 5}다음으로, 이 사전을 사용하여 각 단어에 정수 인덱스를 할당합니다.
In:
import torch
sentence_int = torch.tensor(
[dc[s] for s in sentence.replace(',', '').split()]
)
print(sentence_int)Out:
tensor([0, 4, 5, 2, 1, 3])이제 입력 문장의 정수 벡터 표현을 사용하여 임베딩 레이어를 통해 입력 데이터를 실수 벡터 임베딩으로 인코딩할 수 있습니다. 여기서는 각 입력 단어가 3차원 벡터로 표현되도록 작은 3차원 임베딩을 사용합니다.
임베딩 크기는 일반적으로 수백에서 수천 차원에 이릅니다. 예를 들어, Llama 2는 4,096차원의 임베딩 크기를 사용합니다. 여기서 3차원 임베딩을 사용하는 이유는 순전히 설명을 위해입니다. 이로써 전체 페이지를 숫자로 채우지 않고 개별 벡터를 확인할 수 있습니다.
문장이 6개의 단어로 구성되어 있으므로, 이는 6×3차원 임베딩을 생성합니다.
In:
vocab_size = 50_000
torch.manual_seed(123)
embed = torch.nn.Embedding(vocab_size, 3)
embedded_sentence = embed(sentence_int).detach()
print(embedded_sentence)
print(embedded_sentence.shape)Out:
tensor([[ 0.3374, -0.1778, -0.3035],
[ 0.1794, 1.8951, 0.4954],
[ 0.2692, -0.0770, -1.0205],
[-0.2196, -0.3792, 0.7671],
[-0.5880, 0.3486, 0.6603],
[-1.1925, 0.6984, -1.4097]])
torch.Size([6, 3])가중치 행렬 정의
이제, 트랜스포머 아키텍처의 핵심 요소로 널리 사용되는 Self-Attention 메커니즘인 scaled dot-product attention에 대해 논의해 보겠습니다.
Self-Attention 는 Wq, Wk, Wv라는 세 개의 가중치 행렬을 사용하며, 이 행렬들은 모델 훈련 과정에서 파라미터로 조정됩니다. 이 행렬들은 입력 데이터를 시퀀스의 쿼리, 키, 값 구성 요소로 각각 투영하는 역할을 합니다.
쿼리, 키, 값 시퀀스는 가중치 행렬 W와 임베딩된 입력 x 간의 행렬 곱셈을 통해 얻어집니다.
- 쿼리 시퀀스: q(i) = x(i)Wq for i in sequence 1 … T
- 키 시퀀스: k(i) = x(i)Wk for i in sequence 1 … T
- 값 시퀀스: v(i) = x(i)Wv (i는 시퀀스 1부터 T까지의 인덱스)
인덱스 i는 입력 시퀀스(길이 T) 내의 토큰 인덱스 위치를 의미합니다.

여기서 q(i)와 k(i)는 모두 차원 dk의 벡터입니다. 투영 행렬 Wq와 Wk는 d × dk의 모양을 가지며, Wv는 d × dv의 모양을 가집니다.
(참고로, d는 각 단어 벡터의 크기를 나타냅니다.)
쿼리 벡터와 키 벡터 간의 내적을 계산하기 때문에 이 두 벡터는 동일한 수의 요소를 포함해야 합니다(dq = dk). 많은 LLMs에서는 값 벡터의 크기를 동일하게 설정하여 dq = dk = dv로 합니다. 그러나 결과 컨텍스트 벡터의 크기를 결정하는 값 벡터 v(i)의 요소 수는 임의로 설정될 수 있습니다.
따라서 다음 코드 설명을 위해 dq = dk = 2로 설정하고 dv = 4를 사용하며, 투영 행렬을 다음과 같이 초기화합니다.
In:
torch.manual_seed(123)
d = embedded_sentence.shape[1]
d_q, d_k, d_v = 2, 2, 4
W_query = torch.nn.Parameter(torch.rand(d, d_q))
W_key = torch.nn.Parameter(torch.rand(d, d_k))
W_value = torch.nn.Parameter(torch.rand(d, d_v))(이전의 단어 임베딩 벡터와 유사하게, 차원 dq, dk, dv는 일반적으로 훨씬 더 크지만, 설명을 위해 여기서는 작은 수를 사용합니다.)
비정규화 Attention 가중치 계산
이제 두 번째 입력 요소의 주의 벡터를 계산하는 것에 관심이 있다고 가정해 보겠습니다. 이 경우 두 번째 입력 요소가 쿼리 역할을 합니다.
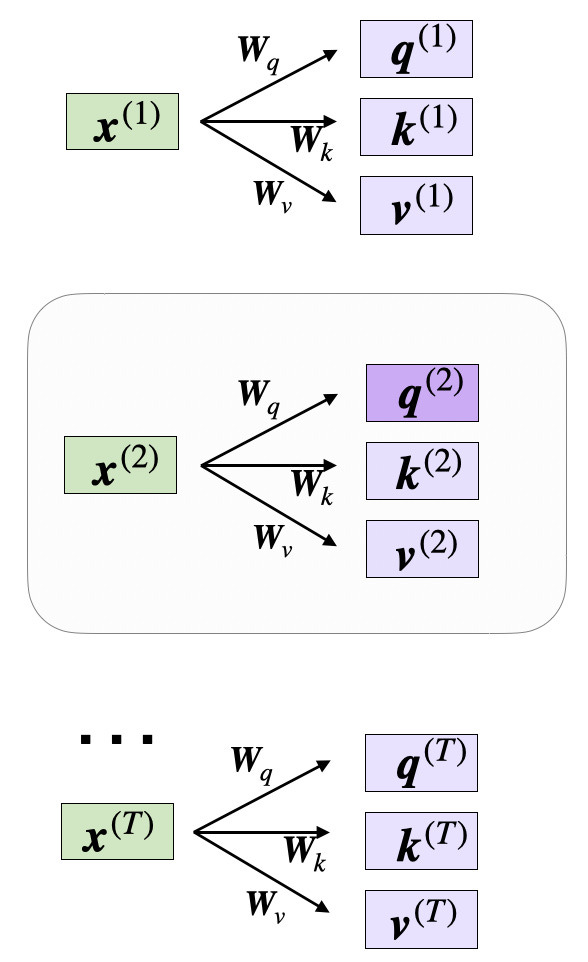
코드에서는 다음과 같이 표시됩니다.
In:
x_2 = embedded_sentence[1]
query_2 = x_2 @ W_query
key_2 = x_2 @ W_key
value_2 = x_2 @ W_value
print(query_2.shape)
print(key_2.shape)
print(value_2.shape)Out:
torch.Size([2])
torch.Size([2])
torch.Size([4])이를 일반화하여 모든 입력에 대한 남은 키 및 값 요소를 계산할 수 있습니다. 이는 다음 단계에서 비정규화 주의 가중치를 계산할 때 필요하기 때문입니다.
In:
keys = embedded_sentence @ W_key
values = embedded_sentence @ W_value
print("keys.shape:", keys.shape)
print("values.shape:", values.shape)Out:
keys.shape: torch.Size([6, 2])
values.shape: torch.Size([6, 4])이제 필요한 모든 키와 값을 확보했으므로 다음 단계로 진행하여 비정규화 주의도 가중치 ω (오메가)를 계산할 수 있습니다. 이는 아래 그림에 표시되어 있습니다.

위 그림에서 보여지듯이, 우리는 쿼리와 키 시퀀스 간의 내적 연산을 통해 ωi,j를 계산합니다. ωi,j = q(i) k(j).
예를 들어, 쿼리와 5번째 입력 요소(인덱스 위치 4에 해당) 간의 정규화되지 않은 주의 가중치를 다음과 같이 계산할 수 있습니다.
In:
omega_24 = query_2.dot(keys[4])
print(omega_24)(참고: ω는 그리스 문자 "오메가"를 나타내는 기호이므로, 위의 코드 변수 이름과 동일한 이름을 사용했습니다.)
Out:
tensor(1.2903)실제 주의 가중치를 계산하기 위해 나중에 필요할 미정규화 주의 가중치 ω를 계산해야 하므로, 이전 그림에 표시된 대로 모든 입력 토큰에 대한 ω 값을 계산해 보겠습니다.
In:
omega_2 = query_2 @ keys.T
print(omega_2)Out:
tensor([-0.6004, 3.4707, -1.5023, 0.4991, 1.2903, -1.3374])Attention 가중치 계산
자기 주의의 다음 단계는 소프트맥스 함수를 적용하여 정규화되지 않은 주의 가중치 ω를 정규화된 주의 가중치 α(알파)로 변환하는 것입니다. 또한, 소프트맥스 함수를 통해 정규화하기 전에 ω를 스케일링하기 위해 1/√{dk}가 사용됩니다. 아래와 같이 표시됩니다.
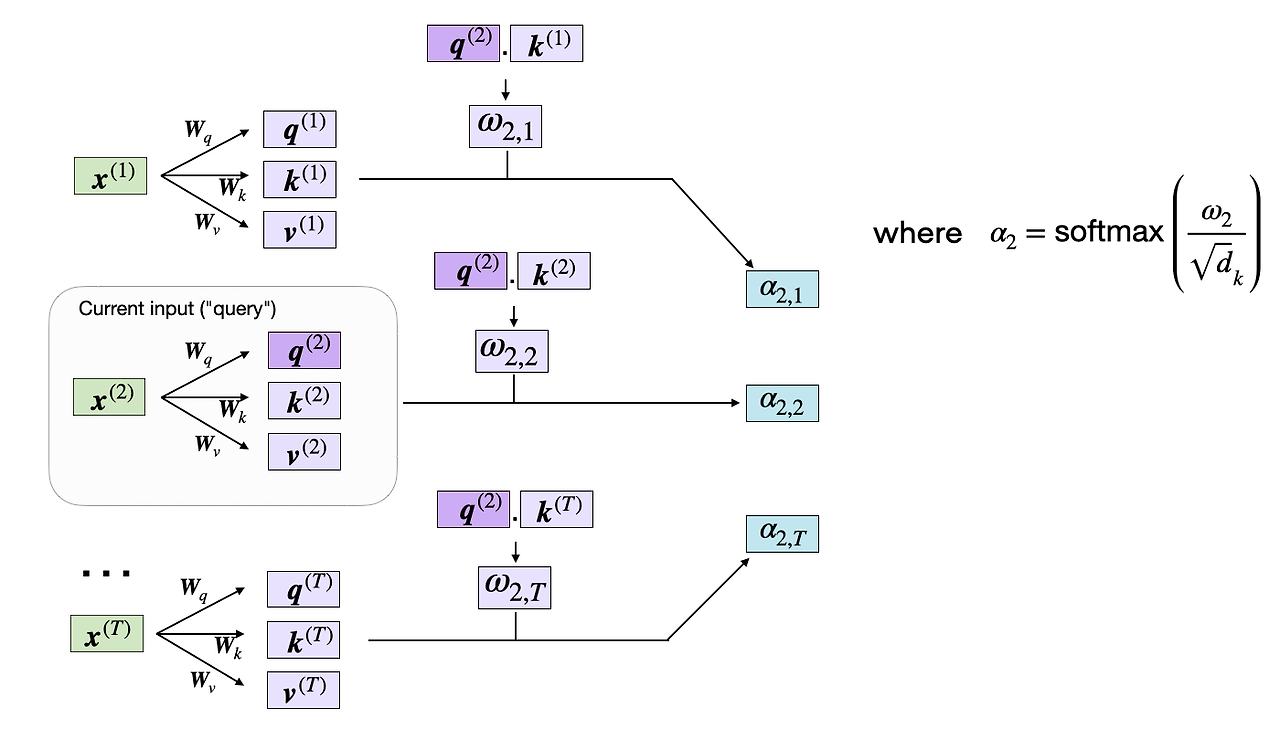
dk에 의한 스케일링은 가중치 벡터의 유클리드 길이가 대략 동일한 규모가 되도록 보장합니다. 이는 주의 가중치가 너무 작거나太大해지는 것을 방지하여, 이는 수치적 불안정성을 초래하거나 훈련 중 모델의 수렴 능력에 영향을 줄 수 있습니다.
코드에서는 주의 가중치의 계산을 다음과 같이 구현할 수 있습니다.
In:
import torch.nn.functional as F
attention_weights_2 = F.softmax(omega_2 / d_k**0.5, dim=0)
print(attention_weights_2)Out:
tensor([0.0386, 0.6870, 0.0204, 0.0840, 0.1470, 0.0229])마지막으로, 마지막 단계는 원래 쿼리 입력 x(2)의 주의 가중치 버전인 컨텍스트 벡터 z(2)를 계산하는 것입니다. 이 컨텍스트 벡터는 주의 가중치를 통해 다른 모든 입력 요소를 컨텍스트로 포함합니다.

코드에서는 다음과 같이 표시됩니다.
In:
context_vector_2 = attention_weights_2 @ values
print(context_vector_2.shape)
print(context_vector_2)Out:
torch.Size([4])
tensor([0.5313, 1.3607, 0.7891, 1.3110])참고로, 이 출력 벡터의 차원 수(dv = 4)는 원래 입력 벡터의 차원 수(d = 3)보다 크며, 이는 이전에 dv > d를 지정했기 때문입니다. 그러나 임베딩 크기 선택인 dv는 임의적입니다.
Self-Attention
이제 이전 섹션에서 설명한 자기 주의 메커니즘의 코드 구현을 마무리하기 위해, 이전 코드를 간결한 SelfAttention 클래스로 요약할 수 있습니다.
In:
import torch.nn as nn
class SelfAttention(nn.Module):
def __init__(self, d_in, d_out_kq, d_out_v):
super().__init__()
self.d_out_kq = d_out_kq
self.W_query = nn.Parameter(torch.rand(d_in, d_out_kq))
self.W_key = nn.Parameter(torch.rand(d_in, d_out_kq))
self.W_value = nn.Parameter(torch.rand(d_in, d_out_v))
def forward(self, x):
keys = x @ self.W_key
queries = x @ self.W_query
values = x @ self.W_value
attn_scores = queries @ keys.T # unnormalized attention weights
attn_weights = torch.softmax(
attn_scores / self.d_out_kq**0.5, dim=-1
)
context_vec = attn_weights @ values
return context_vecPyTorch 컨벤션에 따라 위의 SelfAttention 클래스는 __init__ 메서드에서 자기 주의 매개변수를 초기화하고, forward 메서드를 통해 모든 입력에 대해 주의 가중치와 컨텍스트 벡터를 계산합니다. 이 클래스는 다음과 같이 사용할 수 있습니다.
In:
torch.manual_seed(123)
# reduce d_out_v from 4 to 1, because we have 4 heads
d_in, d_out_kq, d_out_v = 3, 2, 4
sa = SelfAttention(d_in, d_out_kq, d_out_v)
print(sa(embedded_sentence))Out:
tensor([[-0.1564, 0.1028, -0.0763, -0.0764],
[ 0.5313, 1.3607, 0.7891, 1.3110],
[-0.3542, -0.1234, -0.2627, -0.3706],
[ 0.0071, 0.3345, 0.0969, 0.1998],
[ 0.1008, 0.4780, 0.2021, 0.3674],
[-0.5296, -0.2799, -0.4107, -0.6006]], grad_fn=<MmBackward0>)두 번째 행을 보면, 이전 섹션의 context_vector_2에 있는 값과 정확히 일치하는 것을 확인할 수 있습니다. tensor([0.5313, 1.3607, 0.7891, 1.3110]).
Multi-Head Attention
이 게시글 상단(편의상 아래에도 다시 표시됨)에 있는 첫 번째 그림에서, 트랜스포머가 'Multi-Head Attention'이라는 모듈을 사용한다는 것을 확인할 수 있었습니다.

이 "Multi-Head Attention" attention 모듈은 위에서 설명한 Self-Attention 메커니즘(scaled-dot product attention)과 어떻게 관련되어 있나요?
scaled-dot product attention에서 입력 시퀀스는 쿼리, 키, 값을 나타내는 세 개의 행렬을 사용하여 변환되었습니다. 이 세 개의 행렬은 다중 헤드 주의의 맥락에서 single attention head 라고 볼 수 있습니다. 아래 그림은 이전에 설명하고 구현한 이 single attention head 를 요약합니다.

이름에서 알 수 있듯이, 다중 헤드 어텐션은 여러 개의 헤드(각각 쿼리, 키, 값 행렬로 구성됨)를 포함합니다. 이 개념은 컨볼루션 신경망에서 다중 커널을 사용하는 것과 유사하며, 다중 출력 채널을 가진 특징 맵을 생성합니다.

이 개념을 코드로 설명하기 위해, 이전의 SelfAttention 클래스를 위한 MultiHeadAttentionWrapper 클래스를 작성할 수 있습니다.
class MultiHeadAttentionWrapper(nn.Module):
def __init__(self, d_in, d_out_kq, d_out_v, num_heads):
super().__init__()
self.heads = nn.ModuleList(
[SelfAttention(d_in, d_out_kq, d_out_v)
for _ in range(num_heads)]
)
def forward(self, x):
return torch.cat([head(x) for head in self.heads], dim=-1)d_* 매개변수는 SelfAttention 클래스에서 이전과 동일합니다. 여기에서 유일한 새로운 입력 매개변수는 주의 헤드 수입니다.
- d_in: 입력 특징 벡터의 차원.
- d_out_kq: 쿼리 및 키 출력의 차원.
- d_out_v: 값 출력의 차원.
- num_heads: 주의 헤드 수
SelfAttention 클래스는 이 입력 매개변수를 사용하여 num_heads 번 초기화됩니다. 그리고 PyTorch의 nn.ModuleList를 사용하여 이 다중 SelfAttention 인스턴스를 저장합니다.
전파 과정은 입력 x에 대해 self.heads에 저장된 각 SelfAttention 헤드를 독립적으로 적용하는 것을 포함합니다. 각 헤드의 결과는 마지막 차원(dim=-1)을 따라 연결됩니다. 아래에서 실제로 작동하는 모습을 확인해 보겠습니다!
먼저, 설명을 단순화하기 위해 출력 차원이 1인 단일 Self-Attention 헤드를 가정해 보겠습니다.
In:
torch.manual_seed(123)
d_in, d_out_kq, d_out_v = 3, 2, 1
sa = SelfAttention(d_in, d_out_kq, d_out_v)
print(sa(embedded_sentence))Out:
tensor([[-0.0185],
[ 0.4003],
[-0.1103],
[ 0.0668],
[ 0.1180],
[-0.1827]], grad_fn=<MmBackward0>)이제 이 개념을 4개의 어텐션 헤드로 확장해 보겠습니다.
In:
torch.manual_seed(123)
block_size = embedded_sentence.shape[1]
mha = MultiHeadAttentionWrapper(
d_in, d_out_kq, d_out_v, num_heads=4
)
context_vecs = mha(embedded_sentence)
print(context_vecs)
print("context_vecs.shape:", context_vecs.shape)Out:
tensor([[-0.0185, 0.0170, 0.1999, -0.0860],
[ 0.4003, 1.7137, 1.3981, 1.0497],
[-0.1103, -0.1609, 0.0079, -0.2416],
[ 0.0668, 0.3534, 0.2322, 0.1008],
[ 0.1180, 0.6949, 0.3157, 0.2807],
[-0.1827, -0.2060, -0.2393, -0.3167]], grad_fn=<CatBackward0>)
context_vecs.shape: torch.Size([6, 4])위 출력 결과를 보면, 이전에 생성된 single self-attention head가 위 출력 텐서의 첫 번째 열을 나타내고 있음을 확인할 수 있습니다.
multi-head attention 결과는 6×4 차원의 텐서입니다: 입력 토큰이 6개이고 Self-Attention Head가 4개이며, 각 Self-Attention는 1차원 출력을 반환합니다. 이전 Self-Attention 섹션에서도 6×4 차원의 텐서를 생성했습니다. 이는 출력 차원을 1이 아닌 4로 설정했기 때문입니다. 실제 적용 시, SelfAttention 클래스 자체에서 출력 임베딩 크기를 조절할 수 있다면 왜 다중 어텐션 헤드가 필요한가요?
Single Self-Attention Head의 출력 차원을 늘리는 것과 Multi Attention Head를 사용하는 것의 차이는 모델이 데이터를 처리하고 학습하는 방식에 있습니다. 두 접근 방식 모두 모델이 데이터의 다양한 특징이나 측면을 표현하는 능력을 향상시키지만, 그 방식은 근본적으로 다릅니다.
예를 들어, Multi-Head Attention의 각 Attention Head는 입력 시퀀스의 다른 부분에 집중하도록 학습할 수 있으며, 이는 데이터 내의 다양한 측면이나 관계를 포착하는 데 기여합니다. 이 표현의 다양성은 Multi-Head Attention의 성공에 핵심적입니다.
Multi-Head Attention은 특히 병렬 계산 측면에서 더 효율적일 수 있습니다. 각 Head는 독립적으로 처리될 수 있어 GPU나 TPU와 같은 병렬 처리에서 우수한 성능을 발휘하는 현대적 하드웨어 가속기에 적합합니다.
요약하자면, Multi-Head Attention의 사용은 단순히 모델의 용량을 늘리는 것이 아니라 데이터 내의 다양한 특징과 관계를 학습하는 능력을 향상시키는 것입니다. 예를 들어, 7B Llama 2 모델은 32개의 Attention Head를 사용합니다.
Causal Self-Attention
이 섹션에서는 이전에 논의된 Self-Attention 메커니즘을 GPT와 같은 텍스트 생성에 사용되는 디코더 스타일의 대규모 언어 모델(LLM)에 적용하기 위해 Causal Self-Attention 메커니즘으로 적응합니다. 이 Causal Self-Attention 메커니즘은 종종 "masked self-attention"라고도 불립니다. 원본 트랜스포머 아키텍처에서는 이 메커니즘이 "masked multi-head attention" 모듈에 해당합니다. 단순화를 위해 이 섹션에서는 Single Attention Head를 살펴보지만, 동일한 개념은 Multi-Head로 일반화될 수 있습니다.

Causal Self-Attention는 시퀀스 내 특정 위치의 출력이 이전 위치의 알려진 출력에만 기반을 두고 미래 위치의 출력에 의존하지 않도록 보장합니다. 간단히 말해, 각 다음 단어의 예측은 이전 단어에만 의존해야 한다는 것을 보장합니다. GPT와 같은 대규모 언어 모델(LLM)에서 이를 구현하기 위해, 입력 텍스트에서 현재 토큰 이후에 오는 미래 토큰을 마스크 처리합니다.
입력 텍스트에서 미래 토큰을 숨기기 위해 주의 가중치에 인과적 마스크를 적용하는 방법은 아래 그림에 설명되어 있습니다.

Causal Self-Attention를 설명하고 구현하기 위해, 이전 섹션에서 계산된 가중치 없는 주의 점수와 주의 가중치를 사용하겠습니다. 먼저, 이전 Self-Attention 섹션에서 주의 점수를 계산한 과정을 간단히 복습하겠습니다.
In:
torch.manual_seed(123)
d_in, d_out_kq, d_out_v = 3, 2, 4
W_query = nn.Parameter(torch.rand(d_in, d_out_kq))
W_key = nn.Parameter(torch.rand(d_in, d_out_kq))
W_value = nn.Parameter(torch.rand(d_in, d_out_v))
x = embedded_sentence
keys = x @ W_key
queries = x @ W_query
values = x @ W_value
# attn_scores are the "omegas",
# the unnormalized attention weights
attn_scores = queries @ keys.T
print(attn_scores)
print(attn_scores.shape)Out:
tensor([[ 0.0613, -0.3491, 0.1443, -0.0437, -0.1303, 0.1076],
[-0.6004, 3.4707, -1.5023, 0.4991, 1.2903, -1.3374],
[ 0.2432, -1.3934, 0.5869, -0.1851, -0.5191, 0.4730],
[-0.0794, 0.4487, -0.1807, 0.0518, 0.1677, -0.1197],
[-0.1510, 0.8626, -0.3597, 0.1112, 0.3216, -0.2787],
[ 0.4344, -2.5037, 1.0740, -0.3509, -0.9315, 0.9265]],
grad_fn=<MmBackward0>)
torch.Size([6, 6])이전의 Self-Attention 섹션과 마찬가지로, 위의 출력은 6개의 입력 토큰에 대한 쌍별 정규화되지 않은 주의 가중치(주의 점수라고도 함)를 포함하는 6×6 텐서입니다.
이전에는 다음과 같이 소프트맥스 함수를 통해 스케일링된 점곱 주의(scaled dot-product attention)를 계산했습니다.
In:
attn_weights = torch.softmax(attn_scores / d_out_kq**0.5, dim=1)
print(attn_weights)Out:
tensor([[0.1772, 0.1326, 0.1879, 0.1645, 0.1547, 0.1831],
[0.0386, 0.6870, 0.0204, 0.0840, 0.1470, 0.0229],
[0.1965, 0.0618, 0.2506, 0.1452, 0.1146, 0.2312],
[0.1505, 0.2187, 0.1401, 0.1651, 0.1793, 0.1463],
[0.1347, 0.2758, 0.1162, 0.1621, 0.1881, 0.1231],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<SoftmaxBackward0>)위의 6×6 출력은 주의 가중치를 나타내며, 이는 Self-Attention 섹션에서 이전에 계산한 것과 동일합니다.
GPT와 같은 대규모 언어 모델(LLM)에서는 모델을 왼쪽에서 오른쪽으로 한 토큰(또는 단어)씩 읽고 생성하도록 훈련합니다. "Life is short eat desert first"와 같은 훈련 텍스트 샘플이 있다면 다음과 같은 설정이 됩니다. 여기서 화살표 오른쪽의 단어에 대한 컨텍스트 벡터는 해당 단어 자체와 이전 단어만 포함해야 합니다.
- "Life" → "is"
- "Life is" → "short"
- "Life is short" → "eat"
- "Life is short eat" → "desert"
- "Life is short eat desert" → "first"
위와 같은 설정을 구현하는 가장 간단한 방법은 위의 주의 가중치 행렬의 대각선 위쪽에 마스크를 적용하여 모든 미래 토큰을 마스크로 가리는 것입니다. 이 방법은 아래 그림에 표시된 대로, 컨텍스트 벡터(입력에 대한 주의 가중치 합으로 생성됨)를 생성할 때 "미래" 단어가 포함되지 않도록 합니다.
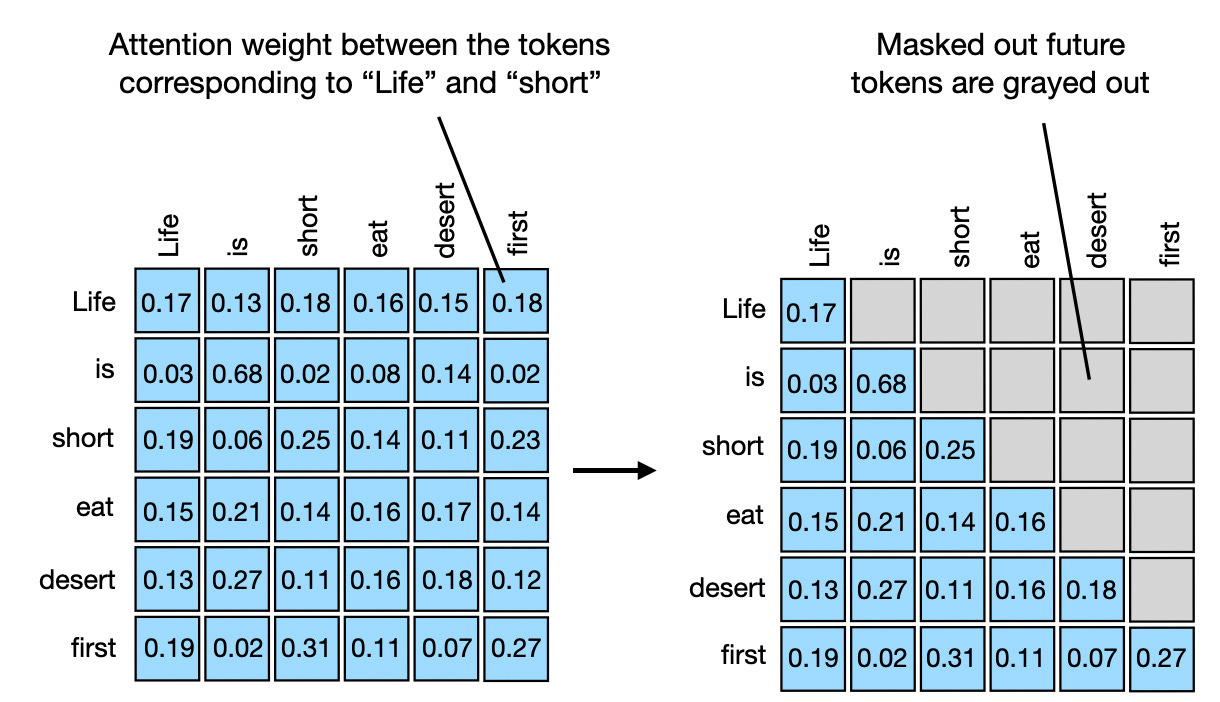
코드에서는 PyTorch의 tril 함수를 사용하여 이를 구현할 수 있습니다. 먼저 이 함수를 사용하여 1과 0으로 구성된 마스크를 생성합니다.
In:
block_size = attn_scores.shape[0]
mask_simple = torch.tril(torch.ones(block_size, block_size))
print(mask_simple)Out:
tensor([[1., 0., 0., 0., 0., 0.],
[1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0.],
[1., 1., 1., 1., 0., 0.],
[1., 1., 1., 1., 1., 0.],
[1., 1., 1., 1., 1., 1.]])다음으로, 이 마스크와 주의 가중치를 곱하여 대각선 위의 모든 주의 가중치를 0으로 설정합니다.
In:
masked_simple = attn_weights*mask_simple
print(masked_simple)Out:
tensor([[0.1772, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0386, 0.6870, 0.0000, 0.0000, 0.0000, 0.0000],
[0.1965, 0.0618, 0.2506, 0.0000, 0.0000, 0.0000],
[0.1505, 0.2187, 0.1401, 0.1651, 0.0000, 0.0000],
[0.1347, 0.2758, 0.1162, 0.1621, 0.1881, 0.0000],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<MulBackward0>)위 방법은 미래의 단어를 가리는 한 가지 방법이지만, 각 행의 주의 가중치가 더 이상 1로 합산되지 않는다는 점을 주의해야 합니다. 이를 완화하기 위해 행을 정규화하여 다시 1로 합산되도록 할 수 있습니다. 이는 주의 가중치에 대한 표준 관례입니다.
In:
row_sums = masked_simple.sum(dim=1, keepdim=True)
masked_simple_norm = masked_simple / row_sums
print(masked_simple_norm)Out:
tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0532, 0.9468, 0.0000, 0.0000, 0.0000, 0.0000],
[0.3862, 0.1214, 0.4924, 0.0000, 0.0000, 0.0000],
[0.2232, 0.3242, 0.2078, 0.2449, 0.0000, 0.0000],
[0.1536, 0.3145, 0.1325, 0.1849, 0.2145, 0.0000],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<DivBackward0>)각 행의 주의 가중치가 이제 1로 합산됩니다.
신경망에서, 특히 트랜스포머 모델과 같은 경우, 주의 가중치를 정규화하는 것은 정규화되지 않은 가중치에 비해 두 가지 주요 이유로 유리합니다. 첫째, 1로 합산되는 정규화된 주의 가중치는 확률 분포와 유사합니다. 이는 입력의 다양한 부분에 대한 모델의 주의도를 비율로 해석하는 데 도움이 됩니다. 둘째, 주의 가중치를 1로 합산하도록 제약함으로써 이 정규화는 가중치와 기울기의 규모를 제어하여 훈련 동력을 개선합니다.
재정규화 없이 더 효율적인 마스킹
위에서 구현한 인과적 자기 주의 절차에서 우리는 먼저 주의 점수를 계산한 후 주의 가중치를 계산하고, 대각선 이상의 주의 가중치를 마스크링한 다음 마지막으로 주의 가중치를 재정규화합니다. 이는 아래 그림에 요약되어 있습니다.

대안으로, 동일한 결과를 달성하는 더 효율적인 방법이 있습니다. 이 접근 방식에서는 주의 점수를 사용하고, 소프트맥스 함수에 입력되기 전에 대각선 위의 값을 음의 무한대로 대체합니다. 이 과정은 아래 그림에 요약되어 있습니다.

이 절차를 PyTorch로 구현하려면 다음과 같이 시작합니다. 먼저 대각선 위의 주의 점수를 마스크 처리합니다.
In:
mask = torch.triu(torch.ones(block_size, block_size), diagonal=1)
masked = attn_scores.masked_fill(mask.bool(), -torch.inf)
print(masked)위의 코드는 먼저 대각선 아래에 0, 대각선 위에 1로 구성된 마스크를 생성합니다. 여기서 torch.triu (상삼각형)은 행렬의 주 대각선 위와 그 위에 있는 요소를 유지하고, 그 아래 요소를 0으로 설정하여 상삼각형 부분을 보존합니다. 반면 torch.tril (하삼각형)은 주 대각선 아래와 그 아래에 있는 요소를 유지합니다.
masked_fill 메서드는 대각선 위의 모든 요소를 마스크 값(1)을 -torch.inf로 대체하며, 결과는 아래에 표시됩니다.
Out:
tensor([[ 0.0613, -inf, -inf, -inf, -inf, -inf],
[-0.6004, 3.4707, -inf, -inf, -inf, -inf],
[ 0.2432, -1.3934, 0.5869, -inf, -inf, -inf],
[-0.0794, 0.4487, -0.1807, 0.0518, -inf, -inf],
[-0.1510, 0.8626, -0.3597, 0.1112, 0.3216, -inf],
[ 0.4344, -2.5037, 1.0740, -0.3509, -0.9315, 0.9265]],
grad_fn=<MaskedFillBackward0>)그 다음에는 평소와 같이 소프트맥스 함수를 적용하여 정규화되고 마스크된 주의 가중치를 얻으면 됩니다.
In:
attn_weights = torch.softmax(masked / d_out_kq**0.5, dim=1)
print(attn_weights)Out:
tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0532, 0.9468, 0.0000, 0.0000, 0.0000, 0.0000],
[0.3862, 0.1214, 0.4924, 0.0000, 0.0000, 0.0000],
[0.2232, 0.3242, 0.2078, 0.2449, 0.0000, 0.0000],
[0.1536, 0.3145, 0.1325, 0.1849, 0.2145, 0.0000],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<SoftmaxBackward0>) 이것이 왜 작동할까요? 마지막 단계에서 적용되는 소프트맥스 함수는 입력 값을 확률 분포로 변환합니다. 입력에 -inf가 존재할 경우, 소프트맥스는 이를 0 확률로 처리합니다. 이는 e^(-inf)가 0에 수렴하기 때문이며, 따라서 이러한 위치는 출력 확률에 아무런 기여를 하지 않습니다.
결론
이 게시글에서는 단계별 코딩 접근법을 통해 자기 주의(self-attention)의 내부 작동 원리를 탐구했습니다. 이를 기반으로, 대규모 언어 변환기(large language transformers)의 핵심 구성 요소인 다중 헤드 주의(multi-head attention)를 살펴보았습니다.
또한 두 개의 서로 다른 시퀀스 간에 적용될 때 특히 효과적인 셀프 어텐션의 변형인 크로스 어텐션을 코딩했습니다. 마지막으로, GPT와 Llama와 같은 디코더 스타일의 대규모 언어 모델(LLM)에서 일관되고 맥락에 맞는 시퀀스를 생성하는 데 필수적인 개념인 인과적 셀프 어텐션을 코딩했습니다.
이 복잡한 메커니즘을 처음부터 코딩함으로써, 트랜스포머와 LLM에서 사용되는 셀프 어텐션 메커니즘의 내부 작동 원리를 잘 이해하셨기를 바랍니다.
(이 기사에서 제시된 코드는 설명을 위한 예시입니다. LLMs 훈련을 위해 셀프 어텐션을 구현할 계획이라면, 메모리 사용량과 계산 부하를 줄이는 최적화된 구현 방식인 Flash Attention 등을 고려하는 것이 좋습니다.)
'AI-ML > LLM' 카테고리의 다른 글
| 논문 읽어보기 - Learning to Reason as Action Abstractions with Scalable Mid-Training RL (0) | 2025.10.05 |
|---|---|
| GPT-OSS 시각화 (0) | 2025.08.21 |
| GPT-2에서 gpt-oss로: 아키텍처적 개선점 분석 (4) | 2025.08.10 |
| 추론 능력(Reasoning) 이해를 위한 대규모 언어 모델(LLMs) (3) | 2025.07.22 |
| 대규모 언어 모델(LLM) 아키텍처 비교 (2) | 2025.07.22 |

